內旋輪線

作者：王一哲
日期：2021/8/9

前言

小時候有一種玩具，將一個小的圓板放在一個大的圓內側，接著用原子筆插在小圓板的某個洞中，用力地將小圓板貼著大圓內側轉動就可以畫出很複雜的圖案，這個玩具的名稱是萬花尺 (spirograph)。

萬花尺（圖片來源：https://upload.wikimedia.org/wikipedia/commons/2/24/Spirograph.jpg）

萬花尺應用到的數學原理名為內旋輪線 (hypotrochoid)，以下是它的參數式。 $$ x(\theta) = (R-r) \cos \theta + d \cos \left( \frac{R-r}{r} \theta \right) $$ $$ y(\theta) = (R-r) \sin \theta - d \sin \left( \frac{R-r}{r} \theta \right) $$
以下是從維基百科上找到的例子，我們接下來試著用 GeoGebra 畫出同樣的圖。

內旋輪線動畫，R = 5，r = 3，d = 5（圖片來源：https://upload.wikimedia.org/wikipedia/commons/f/fa/HypotrochoidOutThreeFifths.gif）

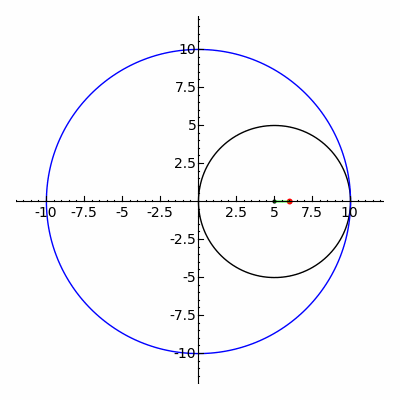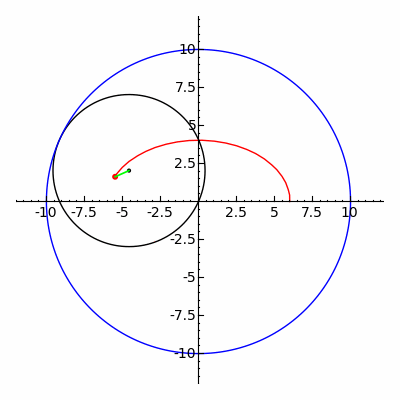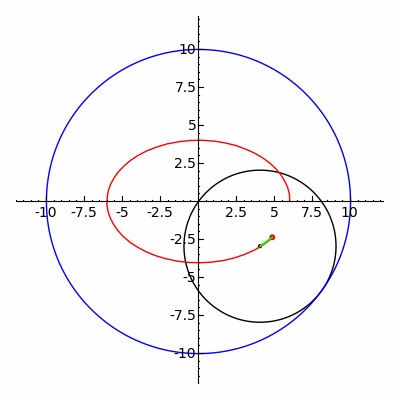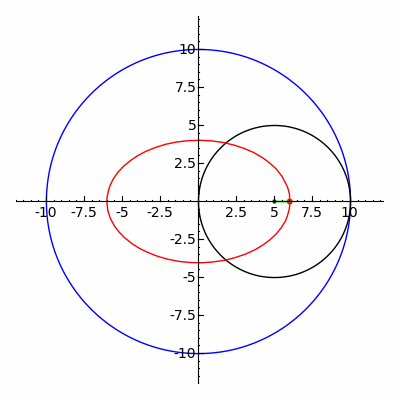
內旋輪線動畫，R = 10，r = 5，d = 1，圖西對 (Tusi couple)（圖片來源：https://upload.wikimedia.org/wikipedia/commons/5/5c/Ellipse_as_hypotrochoid.gif）

繪圖步驟

1. 使用以下指令新增大圓圓心 O₁、小圓半徑 r₂、角速度 ω 、週期 T。

   O_1 = Point({0, 0})
   r_2 = 3
   ω = 0.1
   T = 2 * π /ω
   



2. 使用以下指令新增控制大圓半徑 r₁ 與小圓半徑 r₂ 比值的數值滑桿 ration，如果為了畫出 r₁ : r₂ = 5 : 3 的圖形，可以在數值滑桿上連點滑鼠左鍵兩下，手動輸入量值 5/3。

   ratio = Slider(1.1, 3, 0.1)
   



3. 使用以下指令新增大圓半徑 r₁、小圓圓心 O₃。

   r_1 = ratio * r_2
   O_3 = Point({r_1 - r_2, 0})
   



4. 使用以下指令新增時間的數值滑桿 t，為了使動畫執行時比較流暢，可以適當地調整動畫速度。由於 r₁ : r₂ = 5 : 3 、 d = 5 的圖形小圓需要轉動3次才能畫完，要將 t 的最大值設為 3T；如果是 r₁ : r₂ = 2 : 1、d = 1 的圖形小圓只需要轉動1次就能畫完，可以將 t 的最大值設為 T 即可。

   t = Slider(0, 3*T, T/200)
   



5. 使用以下指令新增旋轉後的小圓圓心 O₂。

   O_2 = Rotate(O_3, ω*t, O_1)
   



6. 使用以下指令新增大圓、小圓。

   c = Circle(O_1, r_1)
   d = Circle(O_2, r_2)
   



繪圖步驟1 - 6



7. 使用以下指令於小圓上新增點A以及繞圓心 O₂ 旋轉的點B。

   A = Point(d)
   B = Rotate(A, -ω (r_1 - r_2) / r_2 * t, O_2)
   



8. 使用以下指令新增通過點B、O₂ 的射線，再於射線上新增要繪製軌跡的點 P。

   f = Ray(B, O_2)
   P = Point(f)
   SetTrace(P, True)
   



繪圖步驟7 - 8


9. 隱藏不需要用到的物件，於數值滑桿 t 上點擊滑鼠右鍵再點選開始動畫，就可以看到以下的動畫。

使用 GeoGebra 繪製的內旋輪線動畫，R = 5，r = 3，d = 5


使用 GeoGebra 繪製的內旋輪線動畫，R = 10，r = 5，d = 1，圖西對 (Tusi couple)



10. 如果想要加上理論曲線，兩種圖形對應的指令如下。

    theory = Curve((r_1 - r_2) cos(θ) + 5*cos((r_1 - r_2) / r_2 θ), (r_1 - r_2) sin(θ) - 5*sin((r_1 - r_2) / r_2 θ), θ, 0, 6*π)
    theory = Curve((r_1 - r_2) cos(θ) + cos((r_1 - r_2) / r_2 θ), (r_1 - r_2) sin(θ) - sin((r_1 - r_2) / r_2 θ), θ, 0, 2*π)
    

使用 GeoGebra 繪製的內旋輪線，R = 5，r = 3，d = 5

使用 GeoGebra 繪製的內旋輪線，R = 10，r = 5，d = 1，圖西對 (Tusi couple)

參考資料

1. 國立台中教育大學科學教育與應用學系科學遊戲實驗室。千變萬花尺。2021年8月9日，取自 http://scigame.ntcu.edu.tw/paper/paper-025.html
2. 維基百科。萬花尺。2021年8月9日，取自 https://en.wikipedia.org/wiki/Spirograph
3. 維基百科。內旋輪線。2021年8月9日，取自 https://en.wikipedia.org/wiki/Hypotrochoid

相關指令的官方說明書

1. 點 https://wiki.geogebra.org/en/Point
2. 數值滑桿 https://wiki.geogebra.org/en/Slider_Command
3. 旋轉 https://wiki.geogebra.org/en/Rotate_Command
4. 圓 https://wiki.geogebra.org/en/Circle_Command
5. 射線 https://wiki.geogebra.org/en/Ray_Command
6. 設定軌跡 https://wiki.geogebra.org/en/SetTrace_Command

---

HackMD 版本連結：https://hackmd.io/@yizhewang/Skj7AMCyt